Перпендикулярные прямые. Перпендикуляр к прямой. Две пересекающиеся прямые образуют четыре неразвернутых угла углы 1, 2, 3 и 4 на рисунке 5. Если один из них прямой, то и остальные углы прямые. Доказательство этого утверждения приведено на рисунке 5. Две пересекающиеся прямые называются перпендикулярными или взаимно перпендикулярными, если они образуют четыре прямых угла. Две пересекающиеся прямые образуют четыре неразвернутых угла углы 1, 2, 3 и 4 на рисунке 53. Если один из них прямой, то и остальные углы. Для краткости вместо слов прямая AC перпендикулярна к прямой BD используют запись AC. Отрезок, соединяющий точку A с точкой H прямой a, называется перпендикуляром, проведенным из точки A к прямой a, если прямые AH и a перпендикулярны рис. Точка H называется основанием перпендикуляра. AH. Мы ввели понятие перпендикуляра, проведенного из данной точки к данной прямой. А есть ли такой перпендикуляр Чтобы ответить на этот вопрос, необходимо провести рассуждение. В математике утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а само рассуждение доказательством теоремы. Обычно сначала формулируют теорему т. Например, когда мы ввели понятие вертикальных углов, то сначала сформулировали теорему хотя и не называли ее теоремой вертикальные углы равны, а затем привели доказательство этой теоремы. Докажем теорему о существовании перпендикуляра к прямой. Перпендикуляр к прямой видеоурок на образовательном портале InternetUrok. Обобщающий урок по геометрии в 7м классе Источник. Перпендикуляр и наклонная. Презентации SliderPoint. Математика 79 класс Геометрия 14,678 views. Презентация по геометрии для 7 класса по теме Перпендикуляр к прямой. На данном уроке вводится понятие перпендикуляра, рассматривается его. Кряк Управление Автотранспортом. Абрамова Юлия. 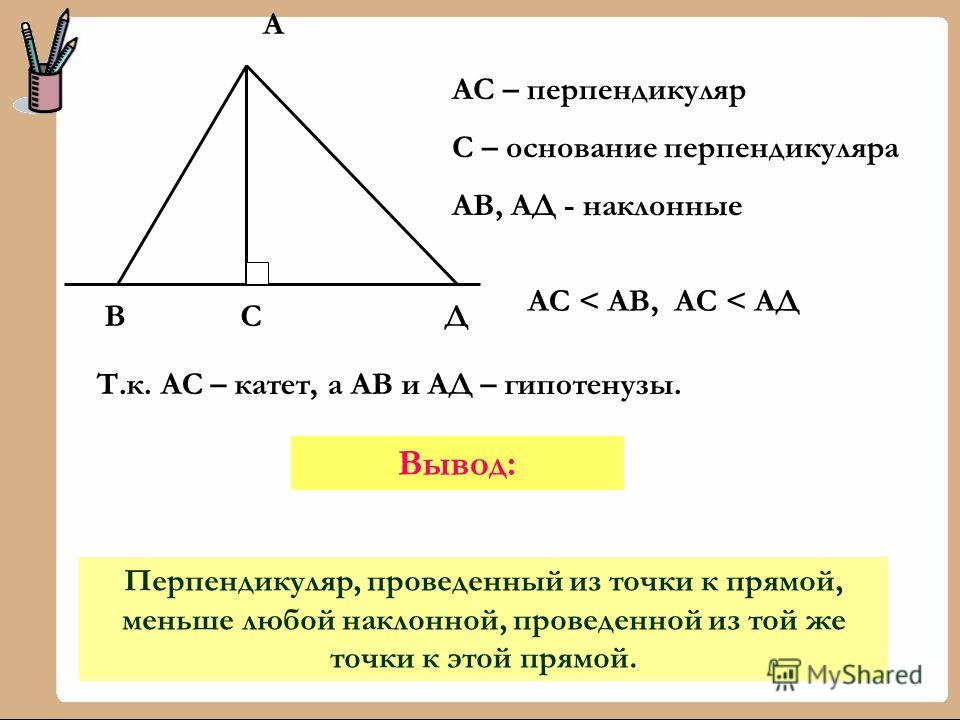Теорема. Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой. Доказательство. Пусть A точка, не лежащая на данной прямой a рис. Докажем, что из точки A можно провести перпендикуляр к прямой a. Мысленно перегнем плоскость по прямой a рис. A, наложилась на другую полуплоскость. При этом точка A наложится на некоторую точку. Обозначим ее буквой B. Разогнем плоскость и проведем через точки A и B прямую. Пусть H точка пересечения прямых AB и a рис. При повторном перегибании плоскости по прямой a точка H останется на месте. Поэтому луч HA наложится на луч HB, и, следовательно, угол 1 совместится с углом 2. Таким образом,. Так как углы 1 и 2 смежные, то их сумма равна 1. Следовательно, отрезок AH перпендикуляр к прямой a. Перпендикуляр К Прямой 7 Класс Презентация' title='Перпендикуляр К Прямой 7 Класс Презентация' />Теорема доказана. Докажем теперь теорему о единственности перпендикуляра к прямой. Теорема. Из точки, не лежащей на прямой, нельзя провести два перпендикуляра к этой прямой. Доказательство. Пусть A точка, не лежащая на данной прямой a см. Докажем, что из точки A нельзя провести два перпендикуляра к прямой a. Предположим, что из точки A можно провести два перпендикуляра AH и AK к прямой a рис. Мысленно перегнем плоскость по прямой a так, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость. При перегибании точки H и K остаются на месте, точка A накладывается на некоторую точку. Обозначим ее буквой B. При этом отрезки AH и AK накладываются на отрезки BH и BK. Перпендикуляр К Прямой 7 Класс Презентация' title='Перпендикуляр К Прямой 7 Класс Презентация' />Углы AHB и AKB развернутые, так как каждый из них равен сумме двух прямых углов. Поэтому точки A, H и B лежат на одной прямой и также точки A, K и B лежат на одной прямой. Таким образом, мы получили, что через точки A и B проходят две прямые AH и AK. Но этого не может быть. Следовательно, наше предположение неверно, а значит, из точки A нельзя провести два перпендикуляра к прямой a. Теорема доказана. Замечание 1. Теоремы о существовании и о единственном перпендикуляре к прямой можно объединить в одну теорему из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. Замечание 2. Из теоремы о единственности перпендикуляра к прямой следует, чтодве прямые, перпендикулярные к одной и той же прямой, не пересекаются. Предположим, что две прямые, перпендикулярные к прямой a, пересекаются в некоторой точке M. Точка M не может лежать на прямой a, так как в этом случае образуется развернутый угол, больший 1. Если же точка M не лежит на прямой a рис. M будут проведены два перпендикуляра к прямой a, что невозможно. Таким образом, две прямые, перпендикулярные к прямой a, не пересекаются.